Least squares
👋 About the exercise session
First of all, let me congratulate you, you have come a long way starting from computing solutions to systems of linear equations all the way up to here - first machine learning application. Yeah, that is right, I just said the fancy word machine learning. 🤖
In this week, our focus will be on solving the following problem:
Based on the provided input \(x\) predict some continuous output \(\hat{y}\)
To make it more concrete, I created a notebook with simple examples that demonstrates all of this. Feel free to check it out, my hope is that it will help you understand least squares more from a practical perspective.
Below, I will first explain theory behind projections. We will then apply this knowledge onto the least squares problem. Last but not the least, Rasmus has made an excellent in depth note about this week’s topic. My goal with this weeks’ notes is to complement and focus more on the big ideas, which should hopefully give you overall good understanding.
📓 Notes
Projections
Consider the following figure (from Rasmus’ note):
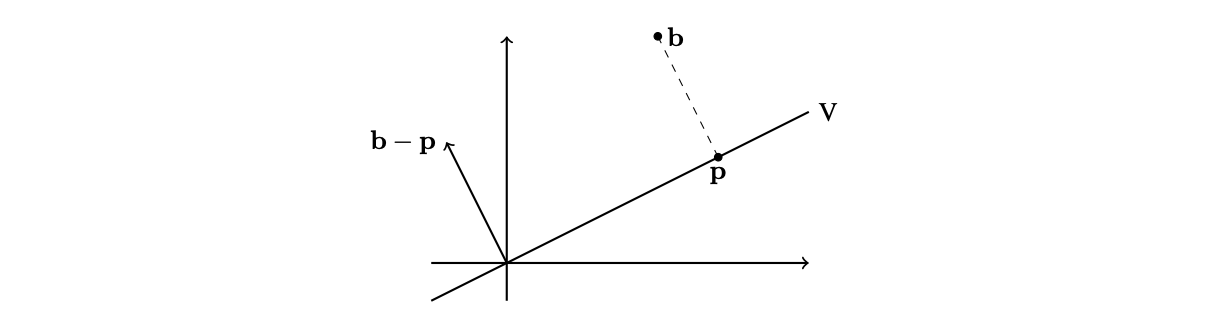
We are given a vector space \(R^2\), corresponding subspace \(V\) (line) and then \(b \in R^2\). Our goal is to find vector \(p \in V\) such that the distance between \(b\) and \(p\) will be minimized. Recall that distance between the two vectors can be computed as:
\[\|\mathbf{b}-\mathbf{p}\|=\sqrt{(x_b-x_p)^2+(y_b-y_p)^2}\]Looking at the formula, it is clear that what really decides about the final distance are the distances between particular coordinates. In the figure, we can see already which point \(p\) has the minimal distance from \(b\). Notice, there is something special about it. If we compute \(b - p\), we get a new vector which is orthogonal to all vectors in \(V\).
From the last week, we know that if vector is orthogonal to all vectors in \(V\), it also must be orthogonal to the basis vectors of \(V\). Therefore, if \(A\) is a matrix whose columns are basis of \(V\), then \(A^T(b - p) = 0\). As a reminder from last week:
\[A^T \mathbf{(b - p)}=\left[\begin{array}{cccc} \mid & \mid & & \mid \\ \mathbf{v}_1 & \mathbf{v}_2 & \ldots & \mathbf{v}_n \\ \mid & \mid & & \mid \end{array}\right]^T \mathbf{(b - p)}=\left[\begin{array}{ccc} - & \mathbf{v}_1^T & - \\ - & \mathbf{v}_2^T & - \\ & \vdots & \\ - & \mathbf{v}_n^T & - \end{array}\right] \mathbf{(b - p)}=\left[\begin{array}{c} \mathbf{v}_1 \bullet \mathbf{(b - p)} \\ \vdots \\ \mathbf{v}_n \bullet \mathbf{(b - p)} \end{array}\right] = 0\]And since \(b - p\) is orthogonal to every basis vector, their dot product must be zero.
So can we exploit \(A^T(b - p) = 0\) to get expression for \(p\)? Of course, we can! But in the least squares problem, we are not interested in the \(p\) itself, but rather its coordinates. Well, we know that since \(p \in V\), it can be written as a linear combination of basis vectors: \(p = A[p]_B\). So, if we substitute for \(p\), we not get the following expression:
\[A^T(b - A[p]_B) = 0\]Now, we just use basic rules of linear algebra to get:
\[A^TA[p]_B = A^Tb\]We need to do one last step:
\[[p]_B = (A^TA)^{-1}A^Tb\]Note that I made one very important assumption here which is that \(A^TA\) is invertible. Rasmus’ in his note proves that this is true, so if you want to know details, feel free to check it out. In addition, since we know that \(p = A[p]_B\), then we can write \(p\) as:
\[p = A[p]_B = A(A^TA)^{-1}A^Tb\]These two equations are the most important outcomes from the projections part. Let me summarize all of this before we move on.
If we are given some vector \(b\) in the original vector space \(R^n\), and our task is to find corresponding vector \(p\) from subspace \(V\) such that the distance between \(b\) and \(p\) is minimized, we can use the following equations to:
- compute the
vector\(p\):
- compute the
coordinatesof vector \(p\) with respect to basis \(B\):
For more detailed explanation, refer to Rasmus’ excellent note.
Least squares: practical perspective
The goal of this section is fairly simple: show you how to apply the projections method to the least squares problem.
Imagine you are given dataset with one feature \(x\) and one response variable \(y\). To help your imagination, you can check this plot out. Your task is to predict \(y\) based on \(x\). For instance I give you as input number of minutes that I ran today and you tell me as a response how many calories I have burnt.
This prediction can be done through some model. Although, this might sound fancy, model can be something as simple as:
Yes, that is an equation of a line with two parameters \(\beta_1\) and \(\beta_0\). So what is missing for us to finally be able to make the predictions? Well, we first need to estimate the model’s parameters. Believe it or not, this can be done through the equation that we found in the previous section:
\[[p]_B = (A^TA)^{-1}A^Tb\]So let’s break it down:
-
Matrix \(A\): this is \(n \times m\) matrix where \(n\) is the number of data points that we are given to estimate the parameters and \(m\) of features in the dataset. Therefore, each row represents a data point (e.g. athlete) and each column represents feature (e.g. weight, # of KMs run, …). In addition, you also always add one more column which is full of ones. I will explain why in a second.
-
column vector \(b\): this is \(n \times 1\) vector which includes expected responses. (e.g. number of calories burnt) Again, \(n\) is the number of data points.
-
column vector \([p]_B\): this will be \(m \times 1\) vector. Do you see? Yes, each value in this vector corresponds to the parameter \(\beta_i\) which we multiply with given feature. In the above example, \(m = 2\) since we have one feature (\(x\)) but we also have the intercept term therefore in total 2 parameters. And this is also the reason why you need to have the last column full of ones - to also obtain estimate for the intercept term.
Very importantly, we do not get some arbitrarily parameters, but we get parameters that minimize the mean squared error:
\[\text{MSE} = \frac{1}{n}\sum_i^n (f(x) - y)^2\]I will go more in depth why this is the case in the next section, but you should already have pretty good intuition from the definition of a projection.
Before we move on, let me make a small comment regards to the order of columns in \(A\) and the order of parameter estimates that you get in \([p]_B\). It is simple, if first column in \(A\) corresponds to the feature \(x\) then the first value in \([p]_B\) is a parameter corresponding to the feature \(x\).
Now, what if we want to make the model more complex? For instance, what if we want to add quadratic term to our model:
\[f(x) = \beta_2x^2 + \beta_1x + \beta_0\]Well, the only difference compare to the previous use case is that we no longer need to estimate 2 parameters, but 3. Therefore, \(A\) must have 3 columns instead of 2. In the previous example, our first column included values of feature \(x\) (e.g. weight) and second column was full of ones (to get the estimate for the intercept). So what values will the new column include? (pause and think about it) It will include the transformation of \(x\), in this case the transformation is the square of \(x\), i.e., \(x^2\).
Last but not the least, as Rasmus wrote in his description of the weekly learning goals, you should also be able to find the parameters for the linear combination of functions. By function, it is meant some transformation on the input variable(s). Well, we have just seen one such example: taking square of \(x\). But let me give you one more example. If we wanted to make our second degree polynomial model even more complex, we could add one more term which is a result of the transformation \(g\):
\[g(x) = log(x) + 42\]So now we would have to add fourth column whose values would correspond to transformation \(g\) applied onto \(x\). As a result our model now looks as:
\[f(x) = \beta_3 g(x) + \beta_2x^2 + \beta_1x + \beta_0\]Hopefully, this section gave you a very good idea about the practical aspect of estimating the model’s parameters. If not so sure, take a look at the this weeks solution sheet. In the following section, I will also try to go over the theoretical information intuition behind least squares, although Rasmus has done allready a pretty great job at that.
Least squares: theoretical intuition
Let me repeat one more time what we concluded in the section about projections since it is important.
If we are given some vector \(b\) in the original vector space \(R^n\), and our task is to find corresponding vector \(p\) from subspace \(V\) such that the distance between \(b\) and \(p\) is minimized, we can use the following equations to:
- compute the
vector\(p\):
- compute the
coordinatesof vector \(p\) with respect to basis \(B\):
Well, in the settings of least squares, we are trying to project vector \(y \in R^n\) to some vector \(\hat{y} \in V\) such that \(y - \hat{y}\) is minimized. Just to crystal clear on the notation, if we are given 5 data points, then \(y\) will have 5 values, and so does \(\hat{y}\) of course.
The real question is how do we define the subspace \(V\)? Well, we want to consider all possible outputs \(\hat{y}\) that we can get based on the provided data points \(x\). Using the example from the practical section, we have some general model \(f(x) = \beta_1x + \beta_0\). If we give it some concrete parameters, then this model gives one particular \(\hat{y}\). Similarly, if we give it some other parameters, we get new \(\hat{y}\). Therefore, more generally, we describe the set of all possible \(\hat{y}\) given some model \(f(x)\) as:
\[V = \{\hat{y} = (f(x_1), \dots, f(x_n)) \text{ | } f(x))\}\]So for instance, if we have 3 data points and we use the quadratic polynomial as our model, then \(V\) is defined as:
\[V = \{\hat{y} = (f(x_1), f(x_2), f(x_3)) \text{ | } f(x) = \beta_2x^2 + \beta_1x + \beta_0)\}\]where \(x_1, x_2, x_3\) are our data points. This means that all vectors in \(\hat{y} \in V\) can be written as:
\[\hat{y} = \beta_2 \begin{bmatrix} x_1^2 \\ x_2^2 \\ x_3^2 \end{bmatrix} + \beta_1 \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} + \beta_0 \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\]Therefore we can write that:
\[V = span(v_1, v_2, v_3)\]where for instance \(v_1\) is:
\[v_1 = \begin{bmatrix} x_1^2 \\ x_2^2 \\ x_3^2 \end{bmatrix}\]and similar logic applies for the other two vectors. From the lecture 4 we know that if we have some subset \(V\) of some vector space \(W\), then the span of this subset is subspace of of \(W\). Therefore, \(V\) is a subspace of \(R^n\) spanned by the three vectors \(v_1, v_2, v_3\). However, does this mean they are also the basis of \(V\)? No! We have to check for linear independence. Or just to be save, we can construct matrix \(A\) where the three vectors will be its columns, take transpose of this matrix and then use Gauss-Jordan elimination to reduce it to row echelon form. All rows with leading 1 will then represent basis vectors of V. We talked about this in detail in the lecture 5. In practice, this is very unlikely to happen, but it is good to double check this.
Once we have the basis of \(V\), then we can use these to construct matrix \(A\) and use it to obtain parameters for our model:
\[[p]_B = (A^TA)^{-1}A^Ty\]where \([p]_B = [\beta_2, \beta_1, \beta_0]\).
⛳️ Learning goals checklist
This week is about learning two main skills:
-
be able to project \(b \in R^n\) onto \(p \in V\) such that the distance between \(b\) and \(p\) is minimized (see the first section)
-
be able to apply the method of least squares to compute best fitting straight lines, nth degree polynomials or other linear combinations of funtions (see the second section for practice, and third section for the theoretical intuition)
Good job for this weeks effort! See you after the fall break, where we will dive into eigenvalues and eigenvectors which we will then use for implementation of the PageRank algorithm.