Exercise 01 solutions

🔹 1.1.11

You are given the following system of equations:

Graph the system, solve it and interpret the results.

Solution

To graph it, let’s first put it in a proper form:

It is up to you how you plot it. I decided to use python:

import matplotlib.pyplot as plt

f1 = lambda x: -2*x + 4
f2 = lambda x: x - 2

x = [i for i in range(-10, 10)]
y1 = [f1(xi) for xi in x]
y2 = [f2(xi) for xi in x]

fig, ax = plt.subplots()

ax.plot(x, y1, label='f1(x) = -2x + 4')
ax.plot(x, y2, label='f2(x) = x - 2')

ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title("System of linear equations")
ax.legend()

# For the cartessian coordinates
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.spines['right'].set_color('none')

fig.savefig('1-1-11.png')

And the result looks like this:

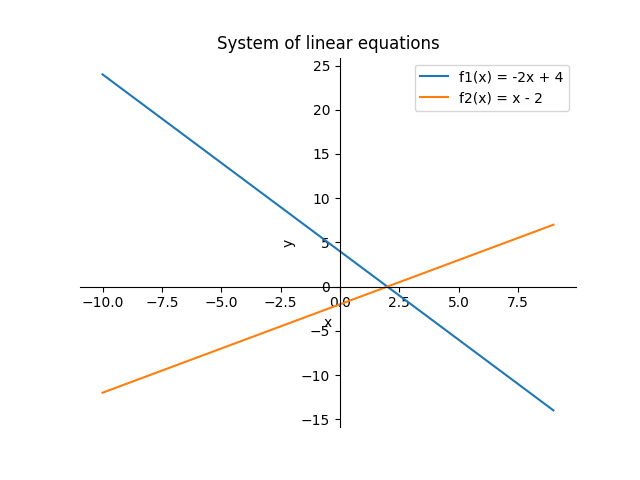
To solve it we can first get it into row echelon form by swapping rows:

And then subtracking double of the first row from the second row, and multiplying the second row by -1:

Then we can use back substitution to obtain value for x which is 2. So as a result we can write:

Looking at the graph, this makes perfect sense, since the two lines intersect at [2, 0].

🔹 1.1.49

See the official solution here.

🔹 1.1.51

See the official solution here.

🔹 1.2.47

A small software corporation borrowed $500,000 to expand its software line. The corporation borrowed some of the money at 3 %, some at 4 % and some at 5 % rate. Use a system of equations to determine how much was borrowed at each rate when the annual interest was $20,500 and the amount borrowed at 4 % was 2.5x the amount borrowed at 3 %. Solve the system using matrices.

Solution (based on the official one)

First of all, we want to construct the system of equations. Let’s therefore first denote the variables we are looking for: x, y, z for the amounts borrowed at 3 %, 4 % and 5 % rates respectively.

Then the system of equations looks as follows:

Before translating it to the matrix form, we format it properly:

And then reduce it to the row echelon form:

Finally, we can then use back substitution to obtain the final result:

Therefore, the corporation borrowed $100,000 at 3 %, $250,000 at 4 % and $150,000 at 5 %.

🔹 1.3.1

See the official solution here.

🔹 1.2.35

See the official solution here.

🔸 Exercise from Rasmus’s notes

For each of the statements below replace the symbol ‘?’ by \(\Longrightarrow\), \(\Longleftrightarrow\) and \(\Longleftrightarrow\), and decide, for each case, if the resulting statement is true or false. If you believe it is false, construct a counter example.

• Ex1: \(x^2=1\) ? \(x=1\)
• Ex2: \(x-y>0\) ? \(x>y\)
• Ex3: \(x y=0\) ? \((x=0 \text{ or } y=0)\)
• Ex4: \((x>0 \text{ and } y>0)\) ? \(xy>0\)

Solution (based on Rasmus’ official solution)

Ex1 If we have \(x^2=1 \Longrightarrow x=1\), it would mean that the only possible solution is 1. A counterexample to this is \(-1\), therefore this statement is not true. If we go the opposite direction, i.e., \(x^2=1 \Longleftarrow x=1\), we can see this statement is true since if x is \(1\), then \(1^2\) is \(1\). The last case (\(\Longleftrightarrow\)) is not neccessary to discuss since we already know that one of the directions does not work.

Ex2 If we modify the first inequation into \(x>y\) ? \(x>y\), we can see that \(x>y \Longrightarrow x>y\) holds true. Similarly, if we adjust the second equation into \(x-y>0\) ? \(x - y > 0\), we can see that \(x-y>0 \Longleftarrow x - y > 0\) is also true. Therefore, \(x-y>0 \Longleftrightarrow x>y\) must also be true.

Ex3 If we start with \(xy=0 \Longrightarrow (x=0 \text{ or } y=0)\), then we can conclude that it is true since the only way product of any two numbers is equal to zero is precisely when either of them is 0 (including both of them of course). The other way around \(xy=0 \Longleftarrow (x=0 \text{ or } y=0)\) also makes since if at least one of the variables is zero, their product must be equal to zero as well. Therefore we can condlude that also \(xy=0 \Longleftrightarrow (x=0 \text{ or } y=0)\) is true.

Ex4 If we consider \((x>0 \text{ and } y>0) \Longrightarrow xy>0\), it means that if two numbers are positive, then their product must also be positive which is true. On the other hand, if product of two numbers is positive, it does not neccessary mean that these numbers are positive, counterexample might be a product of two negative numbers.

🔍 About the page

• Last updated: 12/08/2022
• Unless othewise stated, exercises come from the book: Elementary Linear Algebra, International Metric Edition, Ron Larson
• Purpose: This page was created as part of a preparation for my teaching assistant session in the course Linear algebra and optimization managed by Rasmus Ejlers Møgelberg. Please note that unless othewise stated, the solutions on this page are my own, thus it should not be considered as official solutions provided as part of the course.